gmssl使用

命令行功能

从2.4版开始，GmSSL提供了sm2、sm2utl命令用于SM2相关的计算。

生成SM2私钥

1
$ gmssl sm2 -genkey -sms4 -out sm2.pem

将SM2私钥整数值转换为PEM格式的私钥

1
$ gmssl sm2 -inform text -out sm2.pem

导出SM2公钥

1
$ gmssl sm2 -in sm2.pem -pubout -out sm2Pub.pem

显示SM2私钥的Z值

1
$ gmssl sm2 -genzid -in sm2.pem -id Alice -noout

计算带Z值的杂凑值

1
$ gmssl sm2utl -dgst -in msg.txt -pubin -inkey sm2Pub.pem -id Alice

对消息签名

1
2
$ gmssl sm2utl -sign -in msg.txt -inkey sm2.pem -id Alice -out sig.der
$ gmssl sm2utl -verify -in msg.txt -sigfile sig.der -pubin -in sm2Pub.pem -id Alice

注意，sm2utl是对消息签名，因此支持输入为任意长的消息。pkeyutl也可以进行SM2签名，但是输入是消息的杂凑值

加密解密

1
2
$ gmssl sm2utl -encrypt -in msg.txt -pubin -inkey sm2Pub.pem -out enced.der
$ gmssl sm2utl -decrypt -in enced.der -inkey sm2.pem

和pkeyutl交互

1
2
3
4
5
6
7
8
9
$ gmssl sm2utl -dgst -in msg.txt -pubin -inkey sm2Pub.pem -id Alice -out msg.sm3
$ gmssl sm2utl -sign -in msg.txt -inkey sm2.pem -id Alice -out sm2.sig
$ gmssl pkeyutl -verify -pkeyopt ec_scheme:sm2 -in msg.sm3 -sigfile sm2.sig -pubin -inkey sm2Pub.pem
$ gmssl pkeyutl -sign -pkeyopt ec_scheme:sm2 -in msg.sm3 -inkey sm2.pem -out sm2.sig
$ gmssl sm2utl -verify -in msg.txt -sigfile sm2.sig -pubin -inkey sm2Pub.pem -id Alice
$ gmssl sm2utl -encrypt -in msg.txt -pubin -inkey sm2Pub.pem -out enced.der
$ gmssl pkeyutl -decrypt -pkeyopt ec_scheme:sm2 -pkeyopt ec_encrypt_param:sm3 -in enced.der -inkey sm2.pem
$ gmssl pkeyutl -encrypt -pkeyopt ec_scheme:sm2 -pkeyopt ec_encrypt_param:sm3 -in msg.txt -pubin -inkey sm2Pub.pem -out enced.der
$ gmssl sm2utl -decrypt -in enced.der -inkey sm2.pem

SM2数字签名

SM2数字签名方案中被签名的杂凑值不仅仅是消息的杂凑值，而是签名者身份信息串联上消息的杂凑值，其中签名者身份信息是签名者的可辨别标识字串、椭圆曲线方程系数、生成元和签名者公钥串联后字串的杂凑值。SM2标准中并未说明签名者的可辨别标识字串格式及获得方式，应用可以采用X.509证书中的Subject字段、CN (CommonName)或自行规定。

SM2参数选择

SM2标准中规定采用256比特的椭圆曲线域参数，并采用256比特的密码杂凑算法，并规定某些步骤中须采用SM3。GmSSL的实现支持灵活的参数设定，并支持内置的所有密码杂凑算法，因此应用可以选择安全程度更高的椭圆曲线域参数和密码杂凑算法，如521比特的域参数和SHA-512算法。

SM2公钥加密

SM2公钥加密算法国密公钥加密标准之一，由国家密码管理局与2010年12月公布。SM2公钥加密是一种椭圆曲线公钥加密方案，具体规范可参考《SM2椭圆曲线公钥密码算法 第4部分：公钥加密算法》文本。

SM2公钥加密适用于加密长度较短的数据，如会话密钥和消息报文。SM2公钥加密不仅对数据加密，还提供防篡改的特性，即被篡改的或伪造的密文可以在解密的过程中被检查发现，因此通过SM2公钥加密的消息无需格外的校验机制。消息经过SM2公钥加密后长度会增加不到100字节的长度，加密方在准备缓冲区时需要加以留意。

GmSSL提供了SM2公钥加密的实现。应用应优先通过EVP API调用SM2公钥加密的功能，具体接口使用方法请参考手册页中的EVP_PKEY_encrypt(3)、EVP_PKEY_decrypt(3)等相关函数。

密文编码问题

SM2密文由C1、C2、C3三部分构成，如何对SM2密文进行编码在已经公布的两个标准中有所不同，在早期公布的《SM2椭圆曲线公钥密码算法 第4部分：公钥加密算法》中，SM2密文中的三部分依次输出，没有采用如Tag-Length-Value形式的编码，我们称其为Plain编码。在之后公布的GM/T国标中，SM2密文采用ASN.1/DER方式编码。

GmSSL通过SM2_CIPHERTEXT_VALUE对象来表示密文数据结构，函数SM2_do_encrypt()和SM2_do_decrypt()可以生成SM2_CIPHERTEXT_VALUE对象及对其解密，函数SM2_CIPHERTEXT_VALUE_encode()和SM2_CIPHERTEXT_VALUE_decode()实现该对象的Plain编解码。GmSSL预计还会通过函数i2d_SM2_CIPHERTEXT_VALUE()和d2i_SM2_CIPHERTEXT_VALUE()实现该密文对象的ASN.1/DER编解码，以支持最新的GM/T国密标准。

GmSSL的SM2_encrypt()和SM2_decrypt()在加解密的同时也完成SM2_CIPHERTEXT_VALUE对象的编解码。目前采用Plain编解码，在相应功能完成后会替换为ASN.1/DER编码方案。

SM2密钥交换

推荐椭圆曲线参数

在椭圆曲线密码应用中，通信双方需要预先商定一组称为椭圆曲线域参数的系统参数。椭圆曲线域参数生成需要大量的计算，耗时较长，一旦生成之后可以长期、广泛地使用，因此通常由可信的机构经过反复生成不同的椭圆曲线域参数并挑选出安全性和性能俱佳的公布为标准(推荐参数)，椭圆曲线密码库和应用则会以硬编码的方式内置这些参数。

SM2标准中给出了一个推荐的256比特的素数域椭圆曲线域参数，GmSSL内置了这个椭圆曲线域参数，命名为sm2p256v1。通过GmSSL命令行可以显示该域参数的详细内容如下：

1
$ gmssl ecparam -text -noout -name sm2p256v1 -param_enc explicit

通过ecparam命令可以生成该域参数上的SM2公私钥对。注意，SM2公私要钥对就是标准的椭圆曲线公私要钥对，即可以用于SM2数字签名、密钥交换和公钥加密，也可以用于ECDSA数字签名、ECDH密钥交换和ECIES公钥加密。生成密钥对的命令如下：

1
$ gmssl ecparam -genkey -name sm2p256v1 -out sm2key.pem

如果用户希望在其他支持椭圆曲线密码(但不支持SM2推荐域参数)的密码库或应用中使用这条曲线，可以通过ecparam命令将该域参数导出为标准的PEM格式文件，并导入到目标应用中。

1
$ gmssl ecparam -name sm2p256v1 -param_enc explicit -out sm2p256v1.pem

编程访问SM2推荐椭圆曲线参数

GmSSL内置的SM2推荐曲线可以通过NID NID_sm2p256v1或者字符串"sm2p256v1"索引，在编程时可以通过NID_sm2p256v1生成域参数EC_GROUP对象或者该曲线上的密钥对象EC_KEY。

1
2
3
4
#include <openssl/ec>

EC_GROUP *sm2p256v1 = EC_GROUP_new_by_curve_name(NID_sm2p256v1);
EC_KEY *sm2key = EC_KEY_new_by_curve_name(NID_sm2p256v1);

SM2测试椭圆曲线域参数

SM2标准文本中提供了四个测试用椭圆曲线域参数：

  • 192比特素数域椭圆曲线域参数（sm2p192test)
  • 256比特素数域椭圆曲线域参数（sm2p256test)
  • 193比特二进制域椭圆曲线域参数 (sm2b193test)
  • 257比特二进制域椭圆曲线域参数 (sm2b257test)

crypto/sm2/sm2test.c中提供了这四个参数的定义及生成EC_GROUP对象的代码，应用如果希望使用上述四个参数，可以直接从sm2test.c测试文件中复制相应代码。

SM2 推荐曲线

推荐曲线
  • p：椭圆曲线在质数 p 的有限域 Fp 上的点集合；
  • a：椭圆曲线参数 a 的值；
  • b：椭圆曲线参数 b 的值;
  • n：取值范围，随机整数 d 的取值范围 ；
  • Gx：基点的 x 坐标值，类似于点 P 的 x 坐标值；
  • Gy：基点的 y 坐标值，类似于点 P 的 y 坐标值。

SM2 加密

SM2 加密结果长度是可预测的：对于长度为 n 字节的明文，加密后密文长度为 字节。

加密过程：

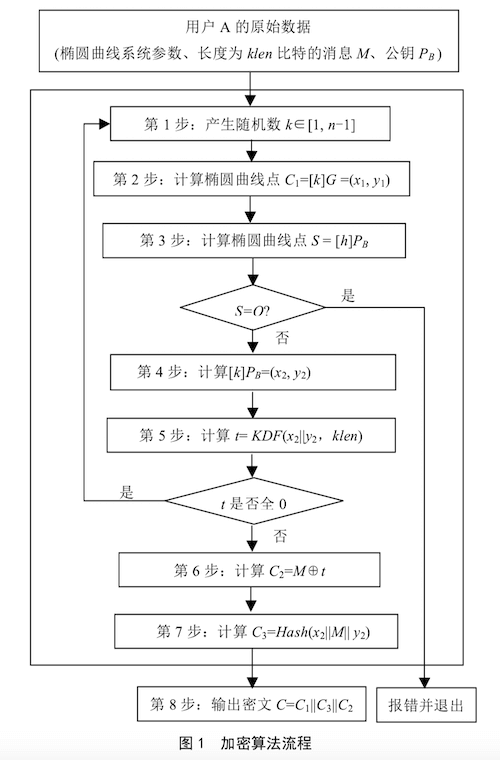
sm2加密

设椭圆曲线为推荐曲线，公钥 Q，原文比特串 M，klen 为 M 的比特长度；

  1. 计算随机椭圆曲线点 ，k 是随机数，G为基点，计算出的倍点 C1 为 64 字节；
  2. 校验公钥 Q，计算椭圆曲线点 ，h为余因子，若S 为无穷点，退出；
  3. 计算椭圆曲线点 ，获取 x2，y2；
  4. 计算 ，，若 t 为全 0 比特串，则返回步骤 1，KDF是 SM2 的密钥派生函数;
  5. 计算 ，对明文加密，C2 是真正的密文，长度和原文相同；
  6. 计算 ，生成杂凑值，用来效验数据，长度 32 字节；
  7. 输出密文 ，C 为密文结果。

注意

  • OpenSSL 的实现使用 ASN.1 编码，因此密文长度可能不固定
  • 由于使用随机数，每次加密结果都不相同

SM2 解密

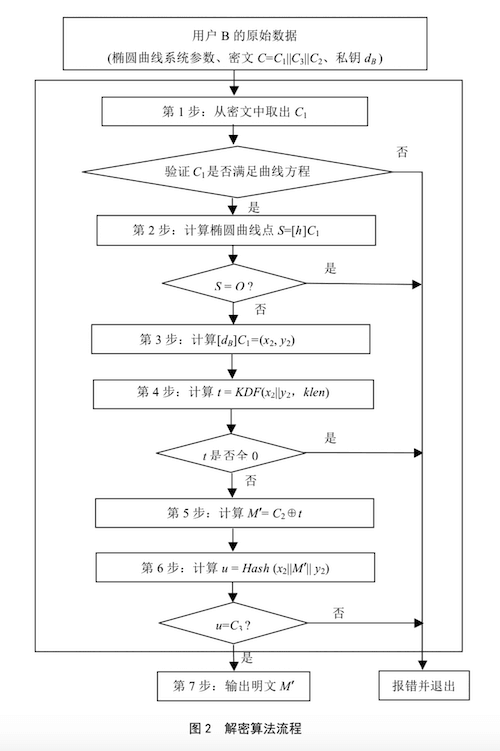
sm2解密

SM2 解密就是逆流程走一遍，注意 OpenSSL 解密要求传入的密文是 ASN1 编码的。

设椭圆曲线为推荐曲线 私钥 d，密文 C（），klen 为密文中 C2 的比特长度。

  1. 从 C 中取出比特串 C1（密文 C 的前 64 字节），将 C1 的数据类型转换为椭圆曲线上的点，验证 C1 是否满足椭圆曲线方程，若不满足则报错并退出;
  2. 计算椭圆曲线点 ，若 S 是无穷远点，则报错并退出；
  3. 计算，将坐标 x2、y2 的数据类型转换为比特串；
  4. 计算 ，，若 t 为全 0 比特串，则报错并退出；
  5. 从 C 中取出比特串 C2，计算 ；
  6. 计算 ，从 C 中取出比特串 C3（密文 C 的后 32 字节），若 ，则报错并退出；
  7. 输出明文 M'，M' 就是解密后的明文。